Misschien heb je de term 'Markov-keten' eerder gehoord, maar tenzij je een paar lessen hebt gevolgd over waarschijnlijkheidstheorie of computerwetenschappelijke algoritmen. Hoe leer je programmeren zonder al de stress Leren programmeren zonder al je stress Misschien heb je besloten om doorgaan met programmeren, of het nu voor een carrière is of gewoon als een hobby. Super goed! Maar misschien begin je je overweldigd te voelen. Niet zo goed. Hier is hulp om uw reis te vergemakkelijken. Lees Meer, je weet waarschijnlijk niet wat ze zijn, hoe ze werken, en waarom ze zo belangrijk zijn.
Het idee van een Markov-keten is een 'under the hood'-concept, wat betekent dat je niet echt hoeft te weten wat ze zijn om ervan te profiteren. U kunt er echter zeker baat bij hebben te begrijpen hoe ze werken. Ze zijn eenvoudig en toch handig op zoveel verschillende manieren.
Dus hier is een spoedcursus - alles wat u moet weten over Markov-kettingen, samengevat in een enkel, verteerbaar artikel. Als je nog dieper wilt graven, probeer dan de gratis informatietheoriscursus op Khan Academy (en overweeg ook andere online cursuswebsites 8 Geweldige websites om gratis college te volgen online 8 Geweldige websites om gratis colleges te volgen online Lees meer).
Markov kettingen 101
Laten we zeggen dat je wilt voorspellen hoe het weer morgen zal zijn. Een echte voorspelling - het soort uitgevoerd door deskundige meteorologen 7 Beste gratis weer-apps voor Android 7 Beste gratis weer-apps voor Android Lees meer - zou honderden of zelfs duizenden verschillende variabelen inhouden die voortdurend veranderen. Weersystemen zijn ongelooflijk complex en onmogelijk te modelleren, tenminste voor leken zoals jij en ik. Maar we kunnen het probleem vereenvoudigen door waarschijnlijkheidsramingen te gebruiken.
Stel je voor dat je toegang had tot dertig jaar weersinformatie. Je begint aan het begin en merkt op dat dag 1 zonnig was. Je blijft doorgaan en merkt op dat dag 2 ook zonnig was, maar dag 3 was bewolkt, toen was dag 4 regenachtig, wat leidde tot een onweersbui op dag 5, gevolgd door zonnige en heldere hemel op dag 6.
Idealiter zou je meer granulair zijn en kiezen voor een analyse van één uur per dag in plaats van een analyse van dag tot dag, maar dit is slechts een voorbeeld om het concept te illustreren, dus wees geduldig!
U doet dit gedurende de gehele 30-jaar durende dataset (die slechts 11.000 dagen zou zijn) en berekent de waarschijnlijkheden van hoe het weer van morgen zal zijn op basis van het weer van vandaag. Als vandaag bijvoorbeeld zonnig is, dan:
- Een kans van 50 procent dat het morgen weer zonnig zal zijn.
- Een kans van 30 procent dat het morgen bewolkt zal zijn.
- Een kans van 20 procent dat het morgen regenachtig zal zijn.
Herhaal dit nu voor alle mogelijke weersomstandigheden. Als het vandaag bewolkt is, wat zijn de kansen dat het morgen zonnig zal zijn, regenachtig, mistig, onweersbuien, hagelbuien, tornado's, enz.? Al snel heb je een heel systeem van waarschijnlijkheden dat je kunt gebruiken om niet alleen het weer van morgen te voorspellen, maar ook het weer van de volgende dag en de volgende dag.
Overgangslanden
Dit is de essentie van een Markov-keten. Je hebt individuele staten (in dit geval weersomstandigheden) waar elke staat kan overstappen naar andere staten (bijvoorbeeld zonnige dagen kunnen overgaan in bewolkte dagen) en die overgangen zijn gebaseerd op waarschijnlijkheden. Als u wilt voorspellen hoe het weer er in een week uitziet, kunt u de verschillende kansen in de komende zeven dagen verkennen en zien welke het meest waarschijnlijk zijn. Dus, een Markov "ketting".
Wie is Markov? Hij was een Russische wiskundige die met het hele idee kwam van één staat die rechtstreeks naar een andere staat leidde op basis van een zekere waarschijnlijkheid, waar geen andere factoren de overgangskans beïnvloeden. Kortom, hij heeft de Markov-keten uitgevonden, vandaar de naamgeving.
Hoe Markovketens worden gebruikt in de echte wereld
Laten we, met de uitleg uit de weg, een aantal van de echte wereldapplicaties verkennen waar ze van pas komen. Je zult verbaasd zijn als je merkt dat je al deze tijd gebruik hebt gemaakt van Markov-ketens zonder het te weten!
Naam genereren
Heb je ooit deelgenomen aan tableop gaming, MMORPG gaming of zelfs fictie schrijven? Je hebt je misschien gekwetst over de naamgeving van je personages (op zijn minst op een bepaald punt) - en toen je gewoon niet kon denken aan een naam die je leuk vindt, heb je waarschijnlijk zijn toevlucht genomen tot een online naamgenerator Create A New Alias With The Beste online naamgenerators [Weird & Wonderful Web] Creëer een nieuw alias met de beste online naamgenerators [Weird & Wonderful Web] Je naam is saai. Gelukkig kun je online gaan en een nieuw alias kiezen met behulp van een van de ontelbare naamgenerators die beschikbaar zijn op Internetz. Lees verder .
Heb je je ooit afgevraagd hoe die naamgenerators werkten? Het blijkt dat velen van hen gebruik maken van Markov-ketens, waardoor het een van de meest gebruikte oplossingen is. (Er zijn andere algoritmen die er zijn die natuurlijk net zo effectief zijn!)
Het enige dat u nodig hebt, is een verzameling brieven waarin elke letter een lijst met mogelijke vervolgbrieven met waarschijnlijkheden bevat. Zo heeft de letter "M" bijvoorbeeld een kans van 60 procent om te leiden naar de letter "A" en een kans van 40 procent om naar de letter "I" te leiden. Doe dit voor een hele reeks andere letters en voer het algoritme uit. Boom, je hebt een naam die logisch is! (Meestal, hoe dan ook.)
Google PageRank
Een van de interessante implicaties van Markov-ketentheorie is dat naarmate de lengte van de keten toeneemt (dat wil zeggen het aantal toestandsovergangen toeneemt), de waarschijnlijkheid dat je op een bepaalde toestand terechtkomt, convergeert op een vast getal, en deze waarschijnlijkheid is onafhankelijk van waar je begint in het systeem.
Dit is buitengewoon interessant als je het hele internet beschouwt als een Markov-systeem waarbij elke webpagina een staat is en de koppelingen tussen webpagina's overgangen met waarschijnlijkheden zijn. Deze stelling zegt in feite dat ongeacht op welke webpagina je begint, je kans om op een bepaalde webpagina X te landen een vaste waarschijnlijkheid is, uitgaande van een 'lange tijd' van surfen .
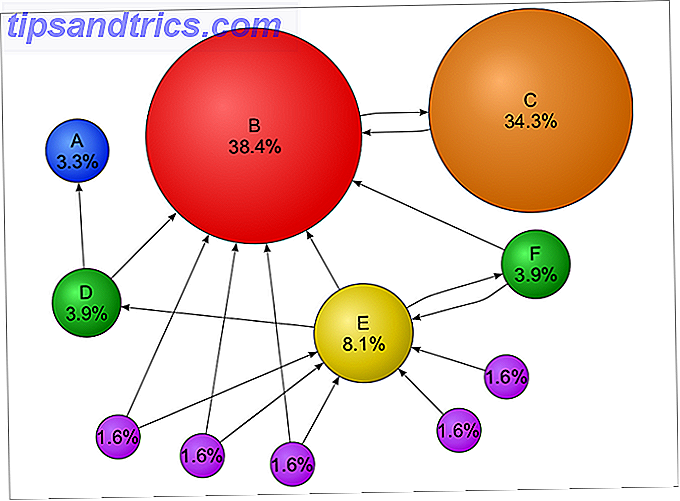
En dit is de basis van hoe Google webpagina's rangschikt. Het PageRank-algoritme is inderdaad een gewijzigde (lees: meer geavanceerde) vorm van het Markov-ketenalgoritme.
Hoe hoger de "vaste waarschijnlijkheid" van het aankomen op een bepaalde webpagina, hoe hoger de PageRank. Dit komt omdat een hogere vaste kans impliceert dat de webpagina veel inkomende links bevat van andere webpagina's - en Google gaat ervan uit dat als een webpagina veel inkomende links bevat, deze waardevol moet zijn. Hoe meer inkomende links, hoe waardevoller het is.
Het is natuurlijk ingewikkelder dan dat, maar het is logisch. Waarom krijgt een site als About.com een hogere prioriteit op pagina's met zoekresultaten? Omdat het erop lijkt dat gebruikers daar meestal aankomen terwijl ze op internet surfen. Interessant, is het niet?
Woordvoorspelling typen
Mobiele telefoons hebben nu al tientallen jaren voorspellend typen, maar kun je raden hoe die voorspellingen zijn gedaan? Of u nu Android gebruikt (alternatieve toetsenbordopties Wat is het beste alternatieve toetsenbord voor Android? Wat is het beste alternatieve toetsenbord voor Android? We bekijken enkele van de beste toetsenborden in de Play Store en testen deze. Meer) of iOS (alternatieve toetsenbordopties 9 Alternatieve iOS-toetsenborden om uw typen gemakkelijker of leuker te maken 9 Alternatieve iOS-toetsenborden om uw typen gemakkelijker of leuker te maken Toen Apple eindelijk optrad als een overbezorgde ouder en toetsenborden van derden introduceerde, ging iedereen keyboard-crazy. Read More), is de kans groot dat uw app naar keuze Markov-ketens gebruikt.
Dit is de reden waarom toetsenbord-apps vragen of ze gegevens over uw typegewoonten kunnen verzamelen. In Google Keyboard is er bijvoorbeeld een instelling met de naam Delen snippets waarin wordt gevraagd fragmenten te delen van wat en hoe u typt in Google-apps om het Google-toetsenbord te verbeteren. In essentie worden je woorden geanalyseerd en verwerkt in de Markov ketenkansen van de app.
Dat is ook waarom toetsenbordapps vaak drie of meer opties presenteren, meestal in volgorde van meest waarschijnlijk tot minst waarschijnlijk. Het kan niet zeker weten wat je vervolgens wilde typen, maar het klopt vaker wel dan niet.
Subreddit-simulatie
Als je Reddit nog nooit hebt gebruikt, moedigen we je aan om in ieder geval dit fascinerende experiment genaamd / r / SubredditSimulator te bekijken.
Simpel gezegd neemt Subreddit Simulator een enorm deel van ALLE opmerkingen en titels op die over de vele gemeenschappen van Reddit zijn gemaakt, en analyseert vervolgens de woord-voor-woord-make-up van elke zin. Met behulp van deze gegevens genereert het woord-naar-woord-waarschijnlijkheden - gebruikt vervolgens die kansen om vanaf het begin titels en opmerkingen te genereren.
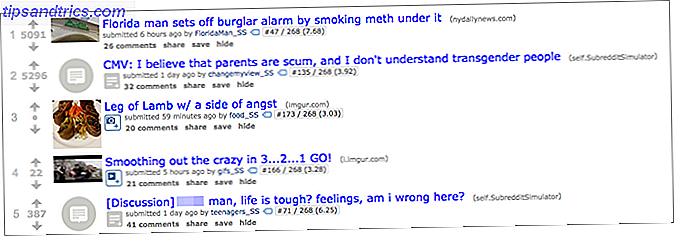
Een interessante laag voor dit experiment is dat opmerkingen en titels worden gecategoriseerd door de community waaruit de gegevens afkomstig zijn, dus de soorten opmerkingen en titels die worden gegenereerd door de dataset van / r / food zijn enorm verschillend van de opmerkingen en titels genereert met / r / gegevensset van voetbal.
En het grappigste - of misschien wel het meest verontrustende - deel van dit alles is dat de gegenereerde opmerkingen en titels vaak niet te onderscheiden zijn van die gemaakt door echte mensen. Het is absoluut fascinerend.
Kent u andere coole toepassingen voor Markov-ketens? Heb je nog vragen die nog beantwoord moeten worden? Laat het ons weten in een reactie hieronder!