Aangezien binary zo absoluut fundamenteel is voor het bestaan van computers, lijkt het vreemd dat we het onderwerp nooit eerder hebben aangepakt - dus vandaag had ik gedacht dat ik een kort overzicht zou geven van wat binary eigenlijk betekent en hoe het in computers wordt gebruikt . Als je je altijd hebt afgevraagd wat het verschil is tussen 8-bit, 32-bit en 64-bit echt is, en waarom het ertoe doet, lees dan verder!
Wat is binair? Het verschil tussen Base 10 en Base 2
De meesten van ons zijn opgegroeid in een wereld van tien getallen, waarmee ik bedoel dat we 10 'basis'- getallen ( 0-9 ) hebben waaruit we alle andere getallen afleiden. Als we die uitgeput hebben, gaan we een niveau omhoog - 10's, 100's, 1000's - deze vorm van tellen wordt vanaf de geboorte in onze hersenen gehamerd. In feite was het pas vanaf de Romeinse tijd dat we begonnen te tellen in basis 10. Voordien was basis 12 het gemakkelijkst, en mensen gebruikten hun knokkels om te tellen.
Wanneer we basis 10 leren op de basisschool, schrijven we vaak de eenheden als volgt uit:
Dus het getal 1990 bestaat eigenlijk uit 1 x 1000, 9 x 100, 9 x 10 en 0 x 1 . Ik weet zeker dat ik base 10 niet verder hoef uit te leggen dan dat.
Maar wat als in plaats van een volledige selectie van 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 om mee te werken als basisgetallen - wat als we alleen 0 hadden, en 1 . Dit wordt basis 2 genoemd ; en het wordt ook vaak binair genoemd . In een binaire wereld kun je slechts tellen van 0, 1 - dan moet je naar het volgende unitniveau gaan.
Tellen in binair getal
Het helpt enorm als we de eenheden uitschrijven wanneer we binair leren. In dit geval wordt in plaats van elke extra eenheid vermenigvuldigd met 10, deze vermenigvuldigd met 2, waardoor we 1, 2, 4, 8, 16, 32, 64 krijgen ... Dus om te helpen berekenen, kunnen we ze als volgt opschrijven:
Met andere woorden, de meest rechtse waarde in een binair getal vertegenwoordigt hoeveel 1-en. Het volgende cijfer links daarvan geeft aan hoeveel 2en. De volgende staat voor hoeveel 4's ... en zo.
Met die kennis kunnen we een tabel met tellingen in binair formaat uitschrijven, met de equivalente basis 10-waarde links aangegeven.
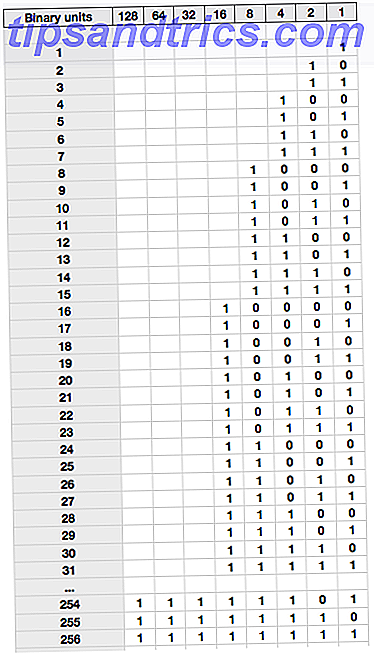
Besteed een moment daarover totdat je precies kunt zien waarom 25 is geschreven als 11001. Je zou in staat moeten zijn om het op te splitsen als zijnde 16 + 8 + 1 = 25.
Naar achteren werken - basis 10 naar binair
Je zou nu in staat moeten zijn om uit te vissen welke waarde een binair getal heeft door een vergelijkbare tabel te tekenen en elke eenheid te vermenigvuldigen. Het omschakelen van een gewone basis 10 naar een binair getal kost wat meer moeite. De eerste stap is het vinden van de grootste binaire eenheid die in het nummer "past". Dus als we bijvoorbeeld 35 doen, dan is het grootste getal uit die tabel dat in 35 past 32, dus we zouden daar een 1 in die kolom hebben. We hebben dan een rest van 3 - die een 2 nodig zou hebben en dan uiteindelijk een 1. Dus we krijgen 100011 .
8-bits, bytes en octetten
De tabel die ik hierboven heb getoond is 8-bit, omdat we maximaal 8 nullen en enen kunnen gebruiken voor ons binaire getal. Het maximale aantal dat we mogelijk kunnen vertegenwoordigen is dus 11111111, of 255 . Dit is de reden waarom om een getal van 0-255 te vertegenwoordigen, we minimaal 8 bits nodig hebben. Octet en Byte is gewoon een andere manier om 8-bits te zeggen. Daarom is 1 byte = 8 bits .
32 versus 64-bit computergebruik
Tegenwoordig hoor je vaak de termen 32-bits en 64-bits versies van Windows, en je weet misschien dat 32-bits Windows slechts maximaal 4 gigabyte RAM kan ondersteunen. Waarom is dat dan?
Het komt allemaal neer op geheugenadressering. Elk stukje geheugen heeft een uniek adres nodig om er toegang toe te hebben. Als we een 8-bits geheugenadresseringssysteem zouden hebben, zouden we maximaal 256 bytes aan geheugen kunnen hebben. Met een 32-bits geheugenadresseringssysteem ( stel je voor dat de bovenstaande tabel wordt uitgebreid tot 32 binaire kolommen ), kunnen we overal naartoe gaan tot 4.294.967.296 ? 4 miljard bytes, of met andere woorden - 4 GIGA- bytes. 64-bit computing verwijdert in wezen deze limiet door ons tot 18 quintillion verschillende adressen te geven - een aantal dat de meesten van ons simpelweg niet kunnen peilen.
IPv4-adressering
De nieuwste zorg in de computerwereld gaat helemaal over IP-adressen IPv6 en de komende ARPAgeddon [Technology Explained] IPv6 & The Corning ARPAgeddon [Technology Explained] Read More, in het bijzonder IPv4- adressen, zoals deze:
- 192.168.0.1
- 200.187.54.22
Ze bestaan in feite uit 4 cijfers, elk vertegenwoordigen een waarde tot 255. Kun je raden waarom? Yep, het hele adres wordt weergegeven door 4 octetten ( 32 bits in totaal ). Dit leek een heleboel mogelijke adressen ( ongeveer 4 miljard in feite ) op het moment dat het internet voor het eerst werd uitgevonden, maar we raken nu snel op de rand omdat alles in ons leven moet worden verbonden. Om dit op te lossen, gebruikt de nieuwe IPv6 in totaal 128 bits, waardoor we ongeveer 340 undecillion ( zet 38 nullen op het einde ) adressen hebben om mee te spelen.
Ik laat het daar vandaag achter, dus ik kan terugkeren naar mijn oorspronkelijke doel, namelijk het schrijven van de volgende Arduino-tutorial - waarin we uitgebreid gebruik maken van een bit-shift register. Ik hoop dat het je vandaag een basiskennis heeft gegeven over hoe binair zo belangrijk is voor computers, waarom dezelfde nummers blijven verschijnen, en waarom het aantal bits dat we moeten representeren een eindige limiet vormt voor de hoeveelheid geheugen, schermgrootte, mogelijke kleur waarden of unieke IP-adressen die voor ons beschikbaar zijn. De volgende keer kijken we naar binaire logica-berekeningen, wat vrijwel allemaal een computerprocessor doet, en ook hoe computers negatieve getallen kunnen vertegenwoordigen.
Opmerkingen? Verwarring? Heb je mijn verklaring gemakkelijk te begrijpen gevonden? Hoe dan ook, neem contact op met de opmerkingen. Ik zal je achterlaten met een binaire grap!
Er zijn slechts 10 soorten mensen in de wereld: zij die binair zijn en degenen die dat niet begrijpen.
Afbeelding tegoed: Shutterstock